この記事は、「Unity Advent Calender 2017」用の記事です。 Unity上でWelch-Powellの**頂点彩色**アルゴリズムを実装し、実際に可視化してみようと思います。
勢いでアドカレに登録したはいいものの、Unityに関して特に公に発信できるようなノウハウが思いつかず、それならば、最近勉強していたグラフ理論をUnity上で展開し、可視化してみようじゃないか!というのが、このテーマ選定のきっかけです。
グラフ理論の中でも今回、頂点彩色を取り上げた理由としては、実装しやすい、かつ、Bloomなどをかけて見た目を調整すれば、規則性のある美しさを少しでも出せるのではないかと考えたからです。
今からつらつらと実装過程を書き連ねますが、勉強のため、間違っている点や改善点があれば、コメントなどで教えていただけると本当に助かります。
前置きが長くなりましたが、Unityで頂点彩色を可視化してみましょう。
頂点彩色とは
隣接するどの2点も異なる色になるようにグラフの頂点を色分けすることを頂点彩色いいます。 今回は触れませんが、グラフの彩色には頂点彩色のほかにも、領域彩色や辺彩色があります。
頂点彩色の様子
これが今回、実際に頂点彩色を可視化した様子です。
・gif Ver

・画像 Ver
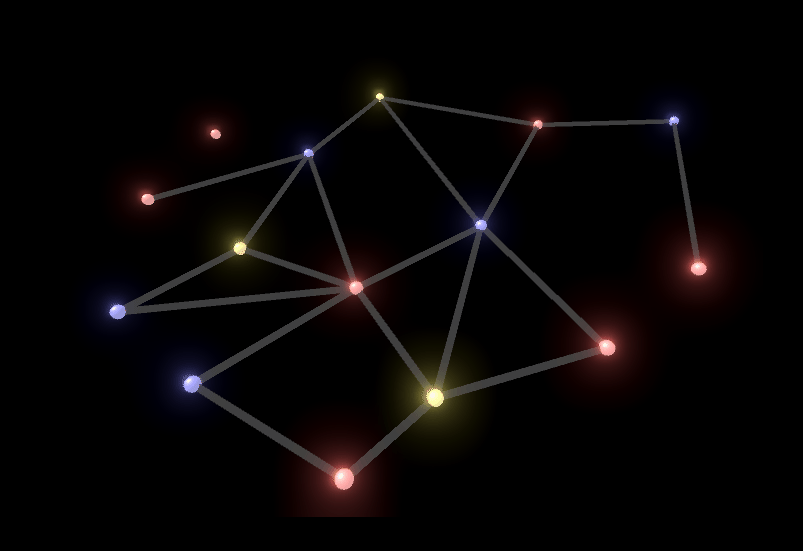
画像verを見てもらえれば分かりやすいですが、任意のノードの隣接ノードはすべて、それぞれが異なる色に塗り分けられていることがわかります。 今回使用したグラフはループを持たない平面グラフといい、必ず4色使えば頂点彩色が可能(=4-頂点彩色可能)です。 上の例では3色で塗り分けができています。
頂点彩色アルゴリズムの実装
では、実際に頂点彩色アルゴリズムを実装していきます。
グラフの作成
まずはグラフを作成します。 今回はUnityエディタ上でグラフを作成しました。 本当はスクリプトから自動生成したかったのですが、いい感じの平面グラフを自動生成するには、実力&時間が足りませんでした、、
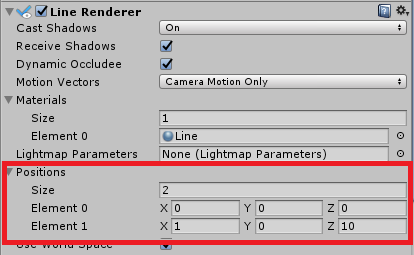
ノードにはプリミティブオブジェクトであるSphereを、辺にはLineRendererを使用しています。 まず適当にノードを散りばめ、その後、座標と座標をつなぐように辺を描きます。
LineRendererはオブジェクト間を繋ぐものではなく、あくまでも座標間を繋ぐものなので、ここもまるで修行僧のようにすべて手動入力しました。
Welch-Powellの頂点彩色アルゴリズム
今回頂点彩色に使用したアルゴリズムは、Welch-Powellの頂点彩色アルゴリズムというものです。 アルゴリズムの流れは以下の通りです。
グラフGの頂点をPi(i=1,2,…,n)とする。
- 各頂点の次数d(Pi)を求める。
- d(pi)を降順に並べる。
- Piに色C1を配色し、2.の順でP1と隣接していない頂点にC1を配色する。さらに2.の順ですでにC1を配色した頂点と隣接していない頂点に順次C1を配色する。
- 2.の順でまだ配色されていないはじめての頂点Pi2に次の色C2を配色し、Pi2と隣接していない頂点でまだ配色されていない頂点に色C2を配色する。
- この操作を2.の頂点がすべて配色されるまで続ける。
このアルゴリズムはループを持たないグラフすべてに使えます。
やさしく学べる離散数学 石村園子[著] を参考、一部引用させていただいてます。
実装
[1., 2.] Welch-Powellの頂点彩色アルゴリズムでは、まず各ノードの次数を計算し、次数が高い順に並べ替える必要があります。
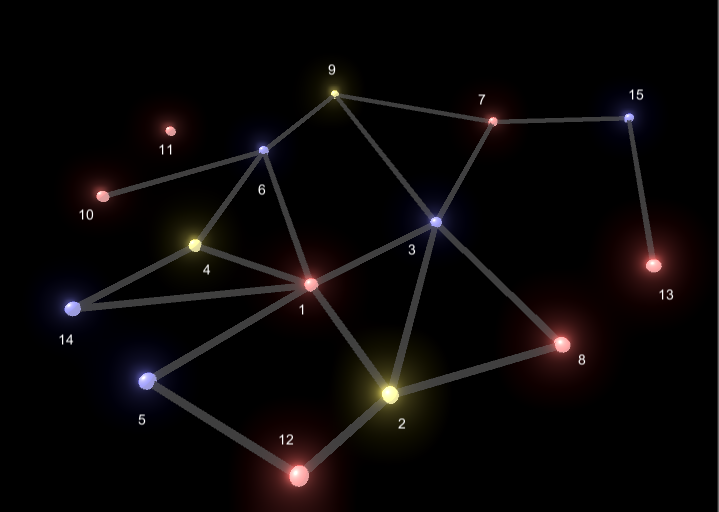
今回15個のノードを用意しました。それぞれにNode1,Node2,Node3,…,Node15といった感じで適当に名前を付け、実際に並べ替えてみます。
すると、例えば、このような感じで並べ替えることができるでしょう。
| 次数 | ノード | 色 |
|---|---|---|
| 6 | Node1 | |
| 5 | Node3 | |
| 4 | Node2 | |
| Node6 | ||
| 3 | Node4 | |
| Node7 | ||
| Node9 | ||
| 2 | Node5 | |
| Node8 | ||
| Node12 | ||
| Node14 | ||
| Node15 | ||
| 1 | Node10 | |
| Node13 | ||
| 0 | Node11 |
[3., 4., 5.] これらのステップを実行に移すには、各ノードの隣接ノード情報が必要です。 Welch-Powellの頂点彩色アルゴリズムの肝でもあります。
下図が、各ノードとその隣接ノードのハッシュテーブルです。
| ノード | 隣接ノード | |||||
|---|---|---|---|---|---|---|
| Node1 | Node2 | Node3 | Node4 | Node5 | Node6 | Node14 |
| Node3 | Node1 | Node2 | Node7 | Node8 | Node9 | |
| Node2 | Node1 | Node3 | Node8 | Node12 | ||
| Node6 | Node1 | Node4 | Node9 | Node10 | ||
| Node4 | Node1 | Node6 | Node14 | |||
| Node7 | Node3 | Node9 | Node15 | |||
| Node9 | Node3 | Node6 | Node7 | |||
| Node5 | Node1 | Node12 | ||||
| Node8 | Node2 | Node3 | ||||
| Node12 | Node2 | Node5 | ||||
| Node14 | Node1 | Node4 | ||||
| Node15 | Node7 | Node13 | ||||
| Node10 | Node6 | |||||
| Node13 | Node15 | |||||
| Node11 | ||||||
ステップを実行していくと、 最初は次数が最も高いNode1に赤を着色、Node1と隣接しないノードの中で最も次数が高いNode7に赤を着色、…を繰り返し、赤を着色できるノードがなくなれば、次の色に切り替えて同じ手順を繰り返します。 そして、すべてのノードの着色が終了するまで繰り返します。
ソースなどはGitHubで公開しています。もし興味があればご覧ください。(コードをごちゃごちゃにしてしまい見づらいです) https://github.com/tanatyu12/GraphColoring/
おわりに
今回は頂点彩色アルゴリズムを愚直に実装し、可視化しました。 今度は、アルゴリズムで演出した規則性にエフェクトや3Dモデルなどを加えてさらに面白い表現をしていきたいです。 もっとUnity力を上げて表現力をつけたいところです。(そろそろシェーダーに手を出したいです)